تعداد زیادی از از پدیدههای طبیعی رشد نمایی دارند. مثلا شما رشد باکتریا را در نظر بگیرید. باکتریای اولی در ظرف یک ساعت ۱ باکتریای دیگه تولید میکند. تعداد باکتریا بعد از یک ساعت ۲تا است. حالا این ۲تا با هم در یک ساعت نفری ۱ باکتریای دیگر تولید میکنند و یک ساعت بعد ما مجموعا ۴تا باکتریا داریم. یک ساعت بعد این ۴تا نفری ۱باکتریا تولید میکنند و ۱۶تا باکتریا داریم. این چرخه تا وقتی غذای باکتریا تمام شود و انرژی برای تولید بیشتر نداشته باشند ادامه دارد. ماجرا برای این هیجان انگیز است که وقتی ۱ باکتریا داشتیم، یک ساعت بعد تعداد باکتریا فقط ضرب ۲ شده بود. اما وقتی ۴ باکتریا داشتیم، بعد از یک ساعت تعداد باکتریا ۱۶تا شده بود. رشد نمایی به حالتی گفته میشود که میزان رشد بستگی به مقدار اولیه دارد. در مثال ما فرمول تعداد باکتریا در هر زمانی این است:
زمان^۲ = تعداد باکتریا
f(t) = 2^t
در آغاز، وقتی زمان = ۰، ما ۱ باکتریا داریم. بعد از یک ساعت، در t = 1 دوتا باکتریا داریم. بعد از ۲ ساعت در t= 2 ما ۴تا باکتریا داریم. بعد از ۲۴ ساعت ما 16,777,216 چیزی نزدیک به ۱۷ ملیون باکتریا داریم.
تعداد مبتلایان کرونا باید رشد نمایی داشته باشد. چون هر قدر تعداد مبتلایان بیشتر باشد ویروس بیشتر و سریعتر پخش میشود و تعداد مبتلایان بیشتر میشود و هر قدر تعداد مبتلایان بیشتر باشد ... این چرخه ادامه دارد :)
رشد نمایی به عدد ثابت اویلر (e) هم ربط دارد. فرمول بالا را میشود به جای ۲ با e هم نوشت. من با درک فلسفهی عدد e مشکل دارم (این برای من غمانگیز است اما شما شانس آوردین :) اگر میدانستم شما حالا توضیحات خوابآور و پراکندهی من را میخواندین :) ) از آنجا که سعی میکنم از هر فرصتی برای فهمیدن عدد e استفاده کنم، امروز از این وبسایت آمار تعداد مبتلایان ِکرونا در دو و نیم ماه گذشته را دانلود کردم. از دادهها نمودار ساختم و خیلی سرسری دادهها را به تابع رشد نمایی برازش کردم.* دادهها گاهی اینقدر به تابع نمایی نزدیکند که حالم از دیدنشان خوب میشود :) نکته اینجاست که معادلهای که من استفاده کردم اصلا پیچیده نیست. هیـــچ معیار اجتماعی و پزشکی را در ساخت این مدل در نظر نگرفتهام. اما با این حال، مدل به حد شگفتانگیزی به دادههای واقعی نزدیک است. یعنی با همین مدل ساده میشود تعداد مبتلایان آینده را تا حد نسبتا دقیقی پیشبینی کرد. اینطور که معلوم است ریاضی دروغ نبوده و چیزهایی که در مورد رشد نمایی به ما گفته بودند راست بوده :)
برای هر کشور در فرمول زیر اعدادی که برای c و k نزدیکترین مدل به آمار را میدادند پیدا کردم :
f(t) = c * et *k
t = زمان
e = عدد اویلر
تصویر پایین تعداد مبتلایان کرونا در هند را از تاریخ ۲۲ جنوری تا ۱۰ آپریل نشان میدهد. دایرههای سرخ آماری است که در دنیای واقعی گرفته شده و خط ِسیاه پیشبینیای است که تابع نمایی در مورد تعداد مبتلایان میکند. محور افقی زمان (به شکل تاریخ) است. محور عمودی تعداد مبتلایان است.
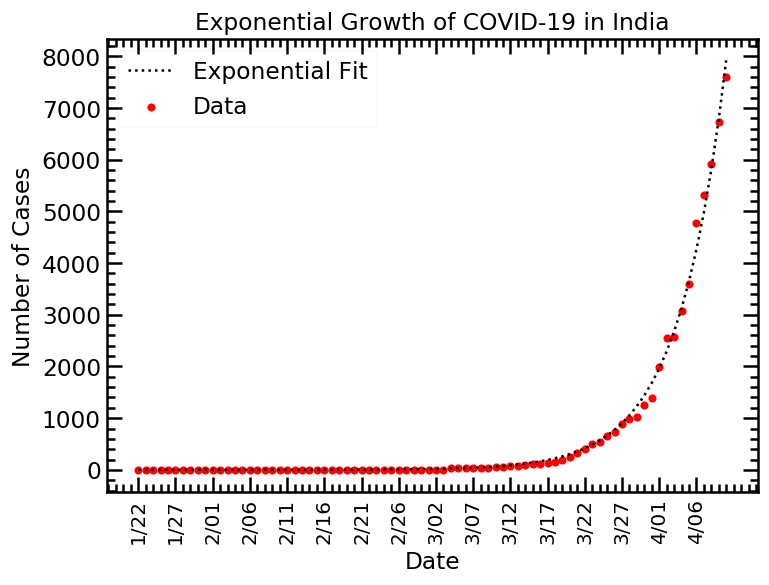
تصویر پایین تمام جزئیات تصویر ِبالا را دارد. تنها تفاوتش این است که آمار از افغانستان است.

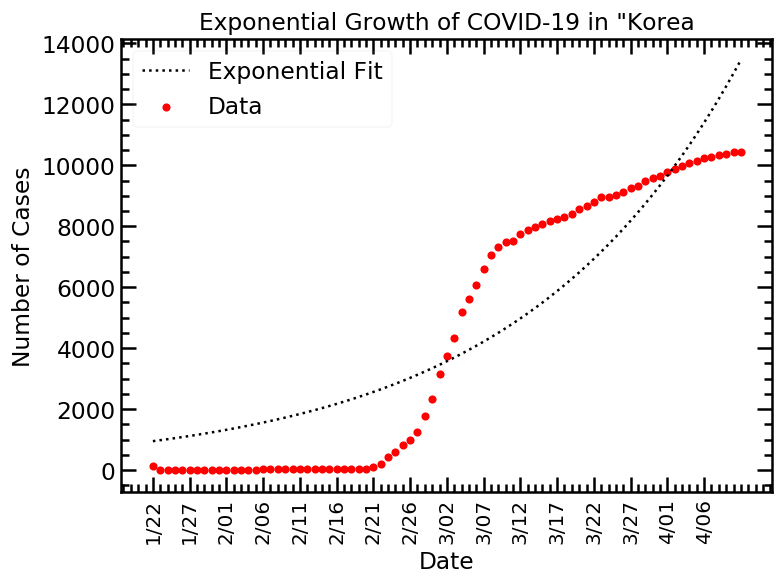
البته این رشد نمایی بعد از اینکه جامعه کرونا را کنترول میکند از بین میرود. تعداد مبتلاها ثابت میماند و دیگر زیاد نمیشوند. برای این مورد به آمار کره جنوبی توجه کنید:
رشد نمایی حدود هفتم مارچ کاملا متوقف میشود و مدل ما پیشبینیگر خوبی برای تعداد مبتلایان آینده نیست.
+ چندتا از این عکسها را به ایستون فرستادم. میگه «یعنی تو تا این حد حوصلهت سر رفته که داری برای کرونا برنامه مینویسی؟ D:»
++ هم درس دارم و هم کار. حوصلهی هیچکدامشان را نداشتم. با خودم گفتم از بیکاری که بهتر است. این تصویرها را برای حدود ۲۵۰ کشور مختلف ساختم :)
*ویکیپدیا میگه Curve fitting به فارسی میشه «برازش منحنی» و من با کمال شرم، واقعا نمیدانم چطور از «برازش منحنی» در جمله استفاده کنم. هدفم این بود که I plotted the data, and tried to fit the data to an exponential growth function of base e.

